Fractals – Chaos Theory, Butterfly Effect, and Psychedelic Images

In the 20th century, scientists like as Benoît Mandelbrot developed a concept to visualise the mathematical phenomenon of complex numbers. The result of their research is as aesthetically fascinating as it is scientific. Their visual representation is known as fractals. Mandelbrot died on 14 October 2010 in Cambridge, Massachusetts.

Chaos Theory and Butterfly Effect: Mathematics, Metaphysics, and Fractal Transcendence

The fractal theory’s philosophical aspect is abut complexity and unpredictability (indetermination). That’s why we call it the chaos theory, or, more poetically, the butterfly effect. Two examples should not be missing from any text on fractals:

Measuring the British coast, you will determine a certain length. But if you repeat the measurement with greater precision, taking into account the circumference of all bays and rocky outcrops, you will measure a much longer coastline. So, theoretically, you could say that the British coast is infinitely long. Of course that is meaningless for practical geography, but this example helps us better understand many phenomena in modern physics and biology.

 

The second and even more popular example states that the flapping of a butterfly’s wings in Europe, through its air movement and a chain reaction of initially small and then increasingly larger consequences, could ultimately trigger a storm in China. This example is similar to Far Eastern stories that have been used to teach the wisdom of Buddhism and the Tao for millennia. After reading popular science articles about chaos theory, many people have begun to seek meanings in it that go beyond classical science. Despite some outlandish theories, such as that of secret messages encoded in fractals, fractals have not only inspired many artists, but chaos theory, through the butterfly example, has also contributed greatly to global thinking and awareness of global ecology.

Fractals from Theory to Practice

So what are fractals good for? As already mentioned, they are ultimately the visualization of a mathematical theory. The resulting images are also used in graphics software to create patterns and backgrounds, including Kai’s Power Tools and various Photoshop plugins. Fractals are presented in large-format illustrated books solely for their aesthetics and beauty.

Fractal formulas are also used to simulate landscapes and to achieve natural-looking representations of organic elements, such as mountains, plants, fire, and hair. Bryce is a landscape generator that was available on PCs from an early stage. Classic C64 computer games like Rescue on Fractalus seem nostalgic today, but they are the first examples of fractal landscapes that arise not from photographs or the hand of an artist, but from mathematical simulation.

In the 1980s, calculating a 320 x 200 pixel fractal on the Commodore 64 could take several hours. Fractal software was rare and was sometimes even typed from books! The more advanced computers of the time, such as the Amiga, Atari ST, or Apple Macintosh, made faster fractal calculations, 3D graphics, and ray tracing (realistic lighting and mirror effects) affordable for ordinary consumers, but high-end workstations were still needed to calculate high-resolution animated computer graphics such as the famous cartoons from Pixar, one of Apple founder Steve Jobs’ companies, which is now part of the Disney corporation. Today, fractal landscape calculation plays a significant role in the production of action and fantasy films.
Apple Men and Julia Sets

In Latin, fractum means a part, as opposed to totum, the whole. Literally, fractal would therefore be the opposite of total. Typically, fractals refer to graphic representations made possible by the application of fractal theory.

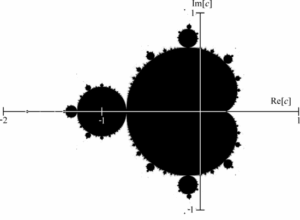
In German, the iconic Mandelbrot set is also known as Apfelmännchen (little apple man) as it remotely resembles an apple shape. Mandelbrot sets are variations of the Julia Sets and they haven only been discovered in 1979 by Benoît Mandelbrot. Their iteration formula (z -> z² + c) is modified in a way that the starting point z0 generally equals the point of origin of the complex number set C. Only mathematicians can possibly memorize this, thus the Mandelbrot set became popular by its more poetic name of Apfelmännchen, and it has been printed on colorful posters and image books.

Interview with Benoît Mandelbrot

more vidoes about fractals, chaos theory, and the butterfly effect (Youtube playlist)

Fractal Software, Self-Similarity, and Animated Fractal Graphics

Fractal software such as Fractint or Iterations made it possible for even users without a theoretical background to enjoy the sight of images no one else had ever seen before – simply by changing new values ​​in predefined formulas. Magnification of the fractal image through recalculation is possible to infinity, continually creating new details and structures that repeat the same or similar form of the original fractal. This aesthetically fascinating property, self-similarity, can also be observed in natural structures such as trees or corals. In the geometry of fractals, self-similarity can be observed in a perfect, abstract way, unaltered by environmental influences. Through simple zoom effects and color animations, computer-calculated fractals can, at their best, be transformed into a psychedelic spectacle similar to that of CTHUGHA and other so-called mind machine software. High-resolution images of particularly beautiful fractals have been published in illustrated books like “The Beauty of Fractals”.